Operations on shapes

Vincent Bonhomme

2018-10-28

Source: vignettes/Momocs_coo.Rmd

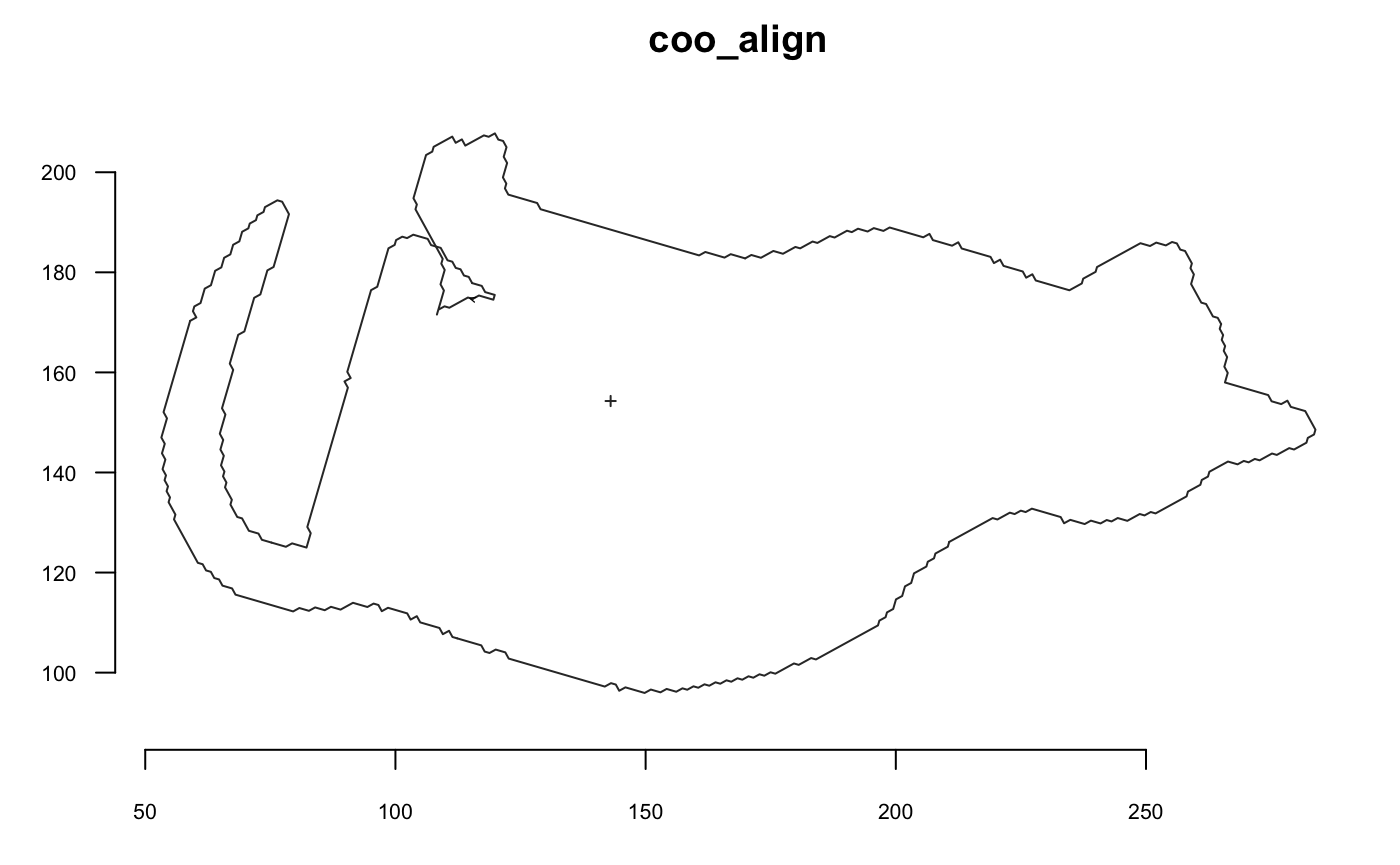
Preamble

In Momocs, a shape is a matrix of (x, y) coordinates. When they are plenty, they are usually gathered in a Coo object which is, essentially, a list with at least a $coo component.

# a single shape
bot[1] %>% is_shp() # tests if it is a 2-col matrix without NAs
## [1] TRUE
##      [,1] [,2]
## [1,]   37  561
## [2,]   40  540
## [3,]   40  529
## [4,]   43  508
## [5,]   46  487
## [6,]   48  477
## [1] "Out" "Coo"
## [1] TRUE
## [1] "list"
## $brahma
##      [,1] [,2]
## [1,]   37  561
## [2,]   40  540
## [3,]   40  529
## [4,]   43  508
## [5,]   46  487
## [6,]   48  477
## 
## $caney
##      [,1] [,2]
## [1,]   53  535
## [2,]   53  525
## [3,]   54  505
## [4,]   53  495
## [5,]   54  485
## [6,]   54  464

Most operations on shapes can also be done on Coo objects. For example, getting the area or centering:

coo_area(bot[1]) # in pixels^2
## [1] 234515
coo_area(bot) %>% head()
##      brahma       caney      chimay      corona deusventrue       duvel 
##    234515.0    201056.5    119459.5    119568.5    165735.5    114015.0

In other words most coo_ functions are actually methods that can actually be passed with a single matrix or a Coo object.

Below, we will distinguish coo_* operations based on whether they return a shape (eg if it is a geometric operation) or a scalar (a single number that can be used as a shape descriptor).

Not all are described but you can obtain a full list of coo_ operations with:

## [1] "coo_align"          "coo_aligncalliper"  "coo_alignminradius"
## [4] "coo_alignxax"       "coo_angle_edges"    "coo_angle_tangent"
## [1] 95

Scalar descriptors of shape

coo_scalar calculate all scalar descriptors included in Momocs. coo_rectilinearity is not included by default since it takes a looot of time to compute.

## # A tibble: 30 x 15
##      area calliper centsize circularity circularityharali… circularitynorm
##     <dbl>    <dbl>    <dbl>       <dbl>              <dbl>           <dbl>
##  1 20030.     319.     87.9        54.4               2.21            4.33
##  2 26078.     311.    103.         32.0               2.47            2.55
##  3 31516      280.     91.2        51.1               2.43            4.07
##  4 14180.     231.     73.0        46.6               2.84            3.71
##  5  9282.     206.     63.4        41.8               2.33            3.32
##  6 24060.     263.     91.2        35.9               3.84            2.85
##  7 14940.     263.     81.5        52.0               2.74            4.14
##  8 33921      352.    109.         35.7               2.83            2.84
##  9 18654      209.     67.3        74.1               2.45            5.89
## 10 36654.     312.     98.3       106.                2.72            8.45
## # ... with 20 more rows, and 9 more variables: convexity <dbl>,
## #   eccentricityboundingbox <dbl>, eccentricityeigen <dbl>,
## #   elongation <dbl>, length <dbl>, perim <dbl>, rectangularity <dbl>,
## #   solidity <dbl>, width <dbl>

Each of the function listed below has its own method that you can used by prefixing it with coo_; see the example below with coo_area.

## area
## calliper
## centsize
## circularity
## circularityharalick
## circularitynorm
## convexity
## eccentricityboundingbox
## eccentricityeigen
## elongation
## length
## perim
## rectangularity
## solidity
## width
coo_area(shapes[4]) # in pixels^2
## [1] 14180.5
coo_area(shapes)
##    arrow     bone buttefly      cat    check    cross      dog     fish 
##  20029.5  26078.5  31516.0  14180.5   9281.5  24060.5  14939.5  33921.0 
##     hand    hands    heart     info     lady     leaf    leaf2    leaf3 
##  18654.0  36653.5  24276.5   8453.5  11541.0  12861.5  16993.5  18301.5 
##    leaf4     moon    morph   parrot    penta   pigeon    plane   puzzle 
##  17748.5  13558.0  28292.0   7894.5  24709.0  23792.5  12649.0  16986.5 
##   rabbit  sherrif    snail     star    tetra umbrella 
##  18915.5  15766.0  26992.5  23132.0  18119.0  16878.5
## # A tibble: 6 x 2
##     area perim
##    <dbl> <dbl>
## 1 20030. 1044.
## 2 26078.  914.
## 3 31516  1269.
## 4 14180.  813.
## 5  9282.  623.
## 6 24060.  929.

Geometric operations

The functions below return shapes, so we exemplify them with graphs. For the sake of clarity/speed we illustrate them on single shape but, again, this can be done on Coo objects.

## will soon be deprecated, see ?pile

## will soon be deprecated, see ?pile

Now we go with a cat and we will extensively use coo_plot. We define a function that will help display side by side the original and transformed cat; when I use p(coo_align), it is equivalent to coo_align(your_shp) or shp %>% coo_align

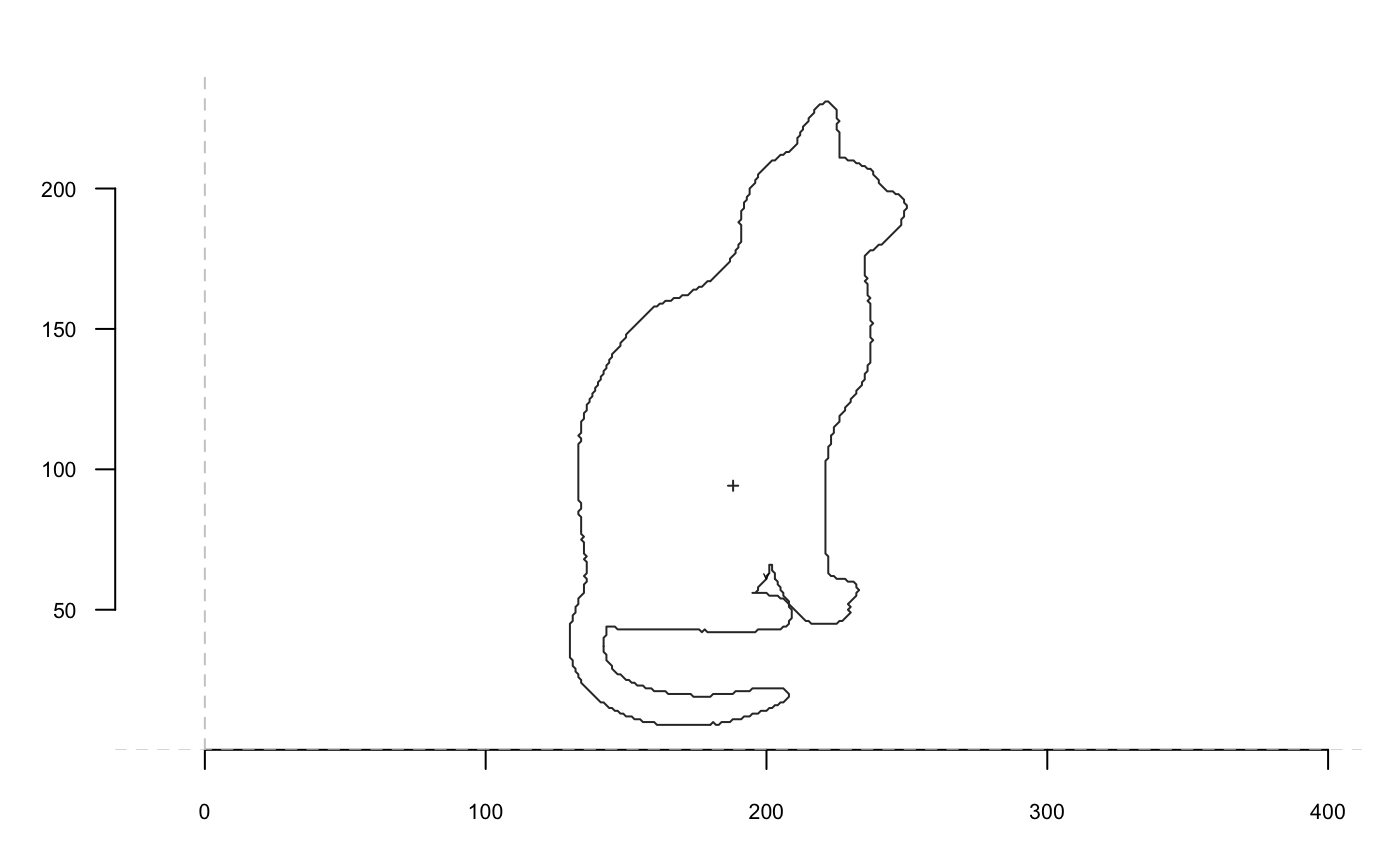
Size

Isotropic

shp %>% coo_plot(main="original cat")

# templating 
shp %>% coo_template(1) %>% coo_plot(ylim=c(-1, 1), main="coo_template"); rect(-0.5, -0.5, 0.5, 0.5)

Anisotropic

shp %>% coo_scalex(2) %>% coo_plot(main="coo_scalex")

shp %>% coo_scaley(3) %>% coo_plot(main="coo_scaley")

shp %>% coo_shearx(1) %>% coo_plot(main="coo_shearx")

shp %>% coo_sheary(1) %>% coo_plot(main="coo_sheary")

Alignment

Based on geometry

shp %>% coo_aligncalliper  %>% coo_plot(main="coo_aligncalliper")

shp %>% coo_alignminradius %>% coo_plot(main="coo_alignminradius")

Translation

shp %>% coo_center %>% coo_plot(main="coo_center") # or coo_centre if you come from UK

shp %>% coo_center %>% coo_trans(x=  5) %>% coo_plot(main="coo_trans")

shp %>% coo_center %>% coo_trans(y= -2) %>% coo_plot(main="coo_trans")

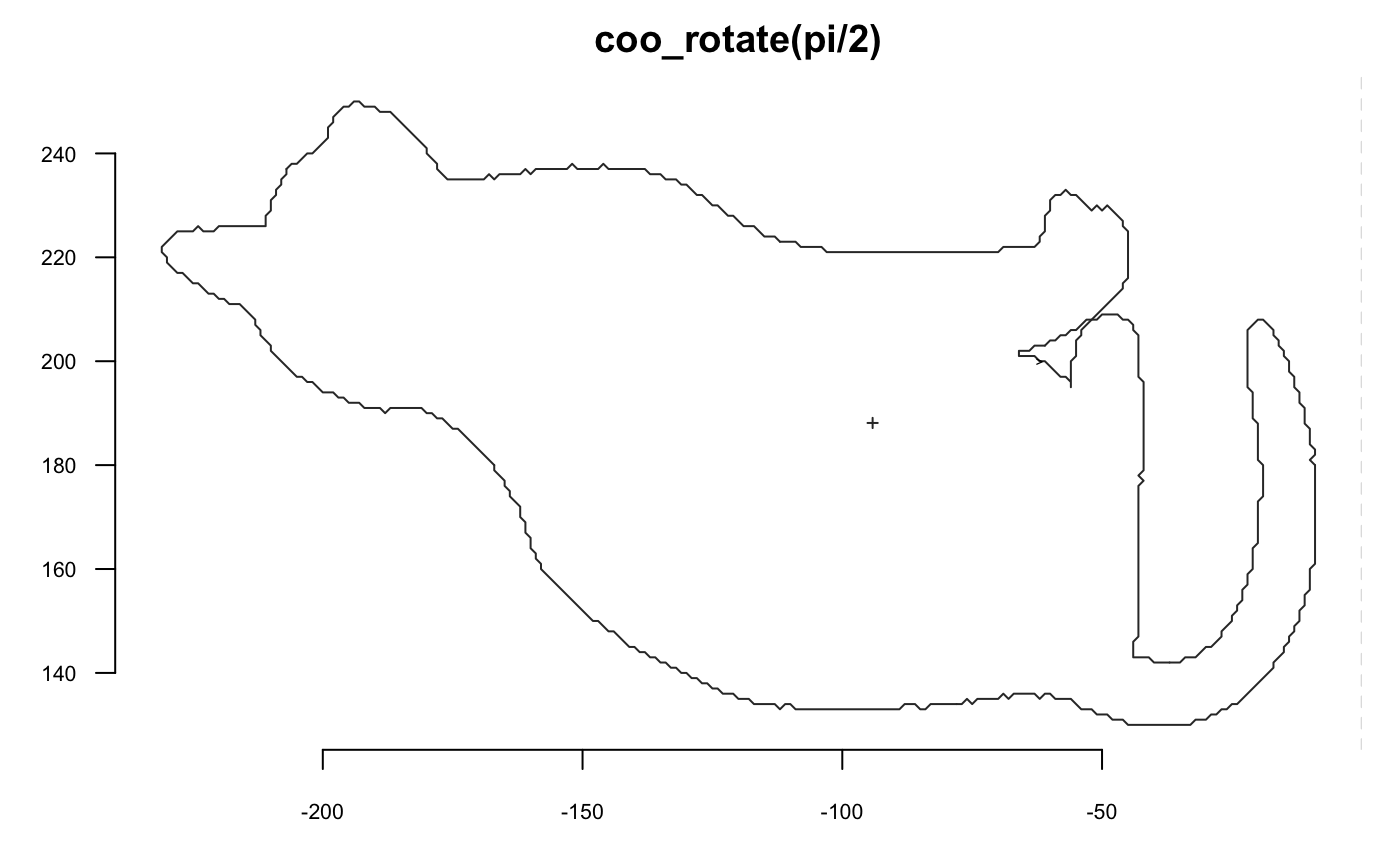
Rotation

shp %>% coo_rotate(pi/2) %>% coo_plot(main="coo_rotate(pi/2)")

shp %>% coo_rotatecenter(-pi/6, center=c(250, 195)) %>% coo_plot(main="coo_rotatecenter") # with center ~on cat's nose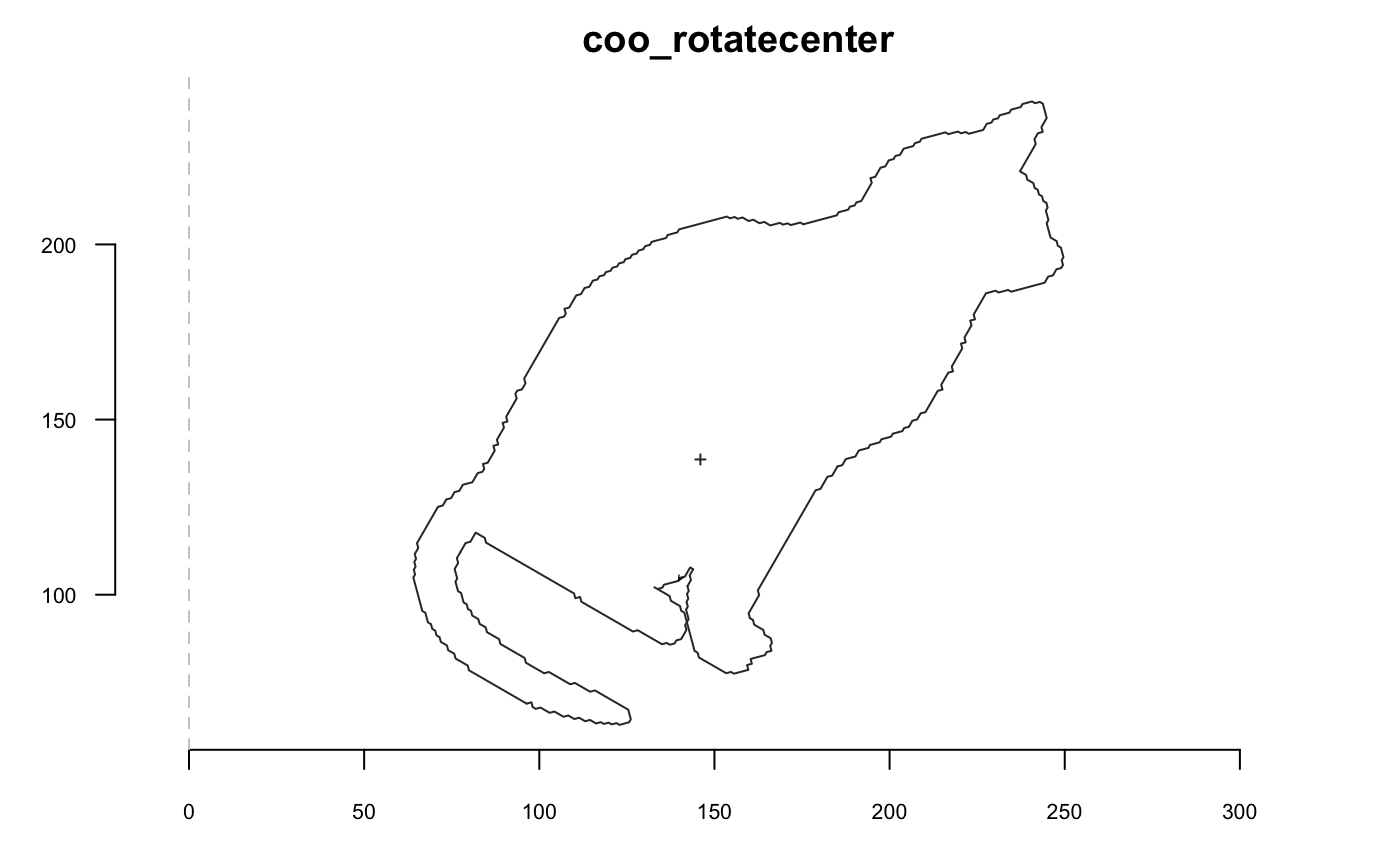

Sampling

## [1] 710
shp %>% coo_sample(36) %>% coo_plot(main="coo_sample")
shp %>% coo_sample_prop(1/20) %>%  coo_plot(main="coo_sample")

shp %>% coo_samplerr(36) %>% coo_plot(main="coo_samplerr") # regular radius

shp %>% coo_sample(36) %>% coo_interpolate(144) %>% coo_plot(points=TRUE, main="coo_interpolate")

Smoothing

shp %>% coo_sample(24) %>% coo_plot(main="a cubist cat")

shp %>% coo_sample(24) %>% coo_smooth(2) %>% coo_plot(main="coo_smooth")

If you have curves, you may prefer not to change first and last points:

olea[1] %>% coo_smooth(12) %>% coo_plot(main="coo_smooth")

olea[1] %>% coo_smoothcurve(12) %>% coo_plot(main="coo_smoothcurve")

Slicing

Based on geometry

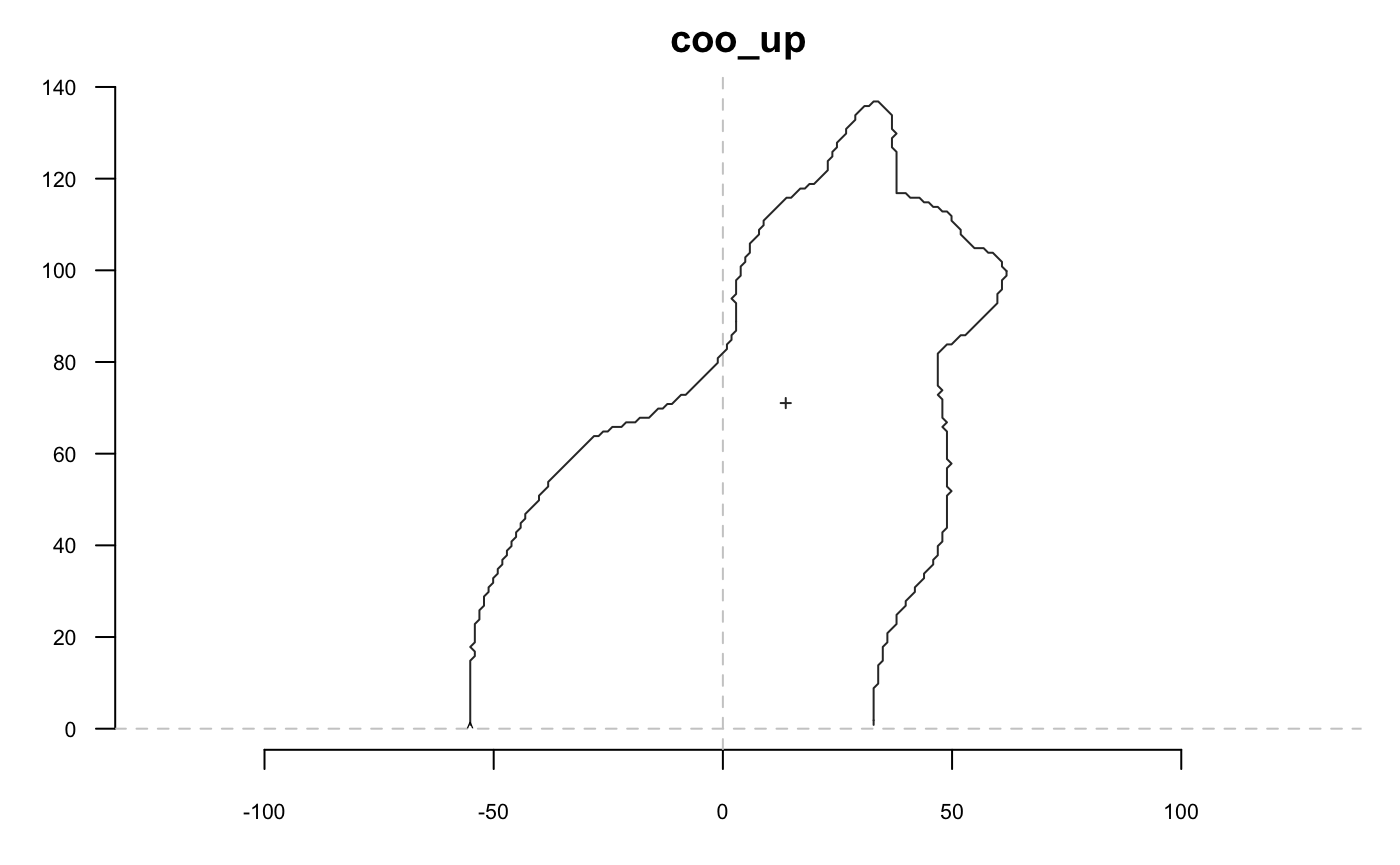
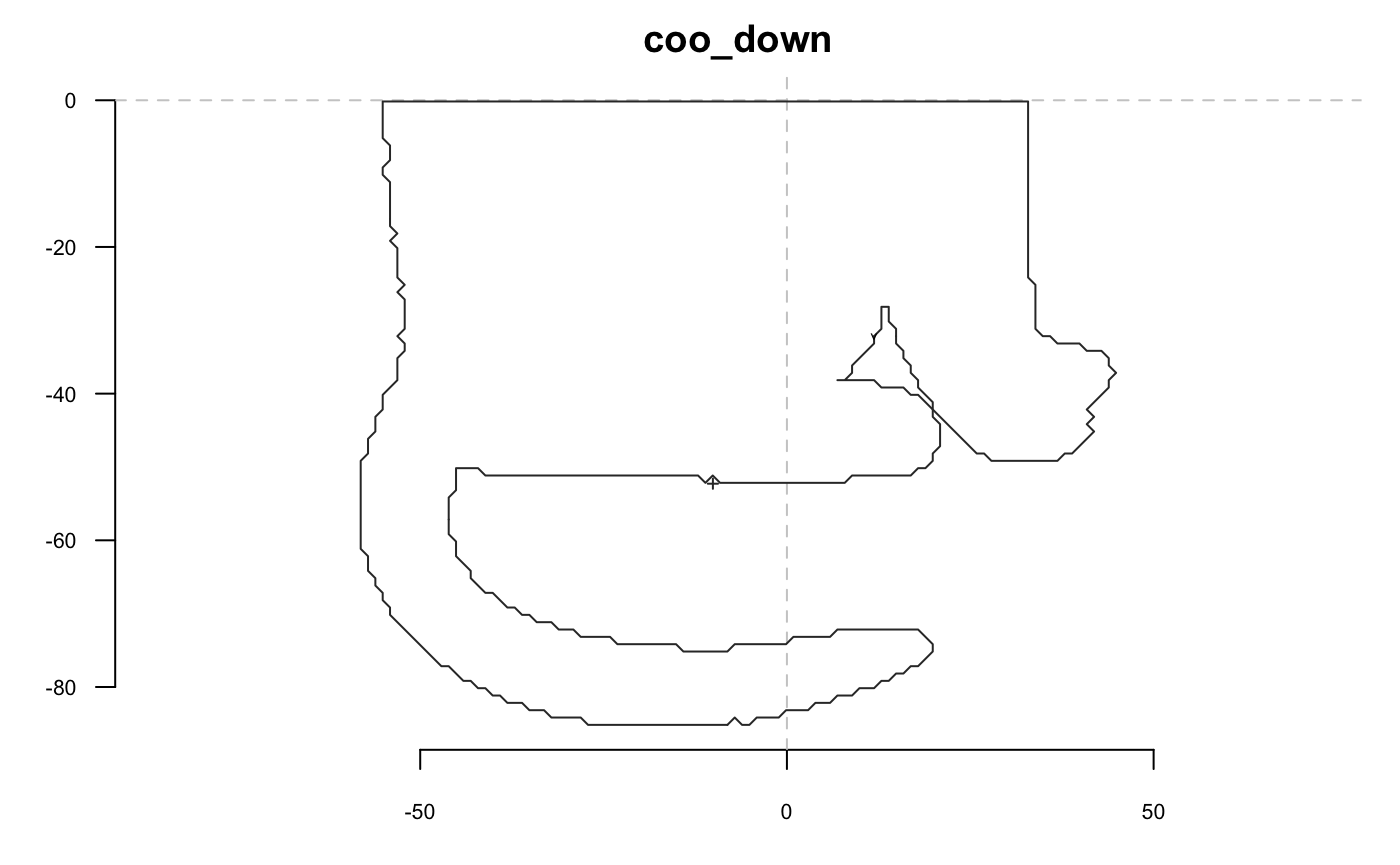
shp %>% coo_center %>% coo_plot(main="centered cat")

If you want to slice but want the first point to be on one end, then coo_slidegap is your friend :

shp %>% coo_center %>% coo_right() %>% coo_slidegap %>% coo_plot(main="coo_right")

Based on landmarks

coo_slice results in at least two shapes. Should be more useful with the argument ldk and within a Coo.

shp %>% coo_center %>% coo_slice(ids=c(93, 516)) %>% Opn %>% panel()

Indexing

Sliding

shp %>% coo_plot(main="original cat", cex.first.point = 2)

shp %>% coo_slide(id=93) %>% coo_plot(main="coo_slide", cex.first.point = 2) # same comment for ldk/Coo as for coo_slice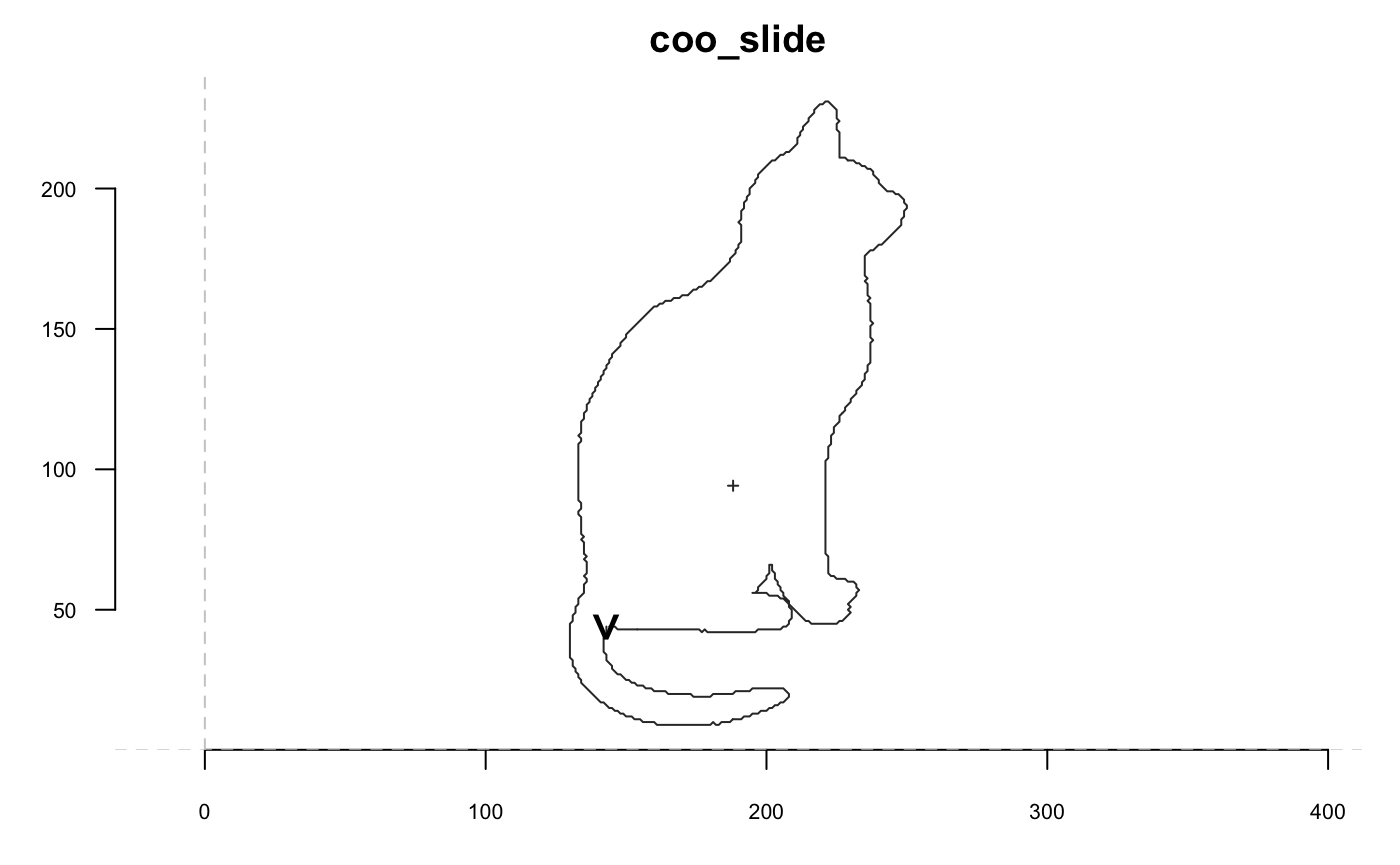

shp %>% coo_slidedirection("right") %>%  coo_plot(main="coo_slidedirection", cex.first.point = 2)

Closing/opening

Trimming/extracting

shp12 %>% coo_trimtop(3) %>% coo_plot(main="coo_trimtop")

shp12 %>% coo_trimbottom(3) %>% coo_plot(main="coo_trimtop")

shp12 %>% coo_trim(3) %>% coo_plot(main="coo_trim")

shp %>% coo_extract(93:516) %>% coo_plot(main="coo_extract")

Reversing

shp12 %>% coo_rev %>% coo_plot(main="coo_rev", cex.first.point = 2)

Misc

A side effect of coo_dxy is to set the first point on (0, 0)

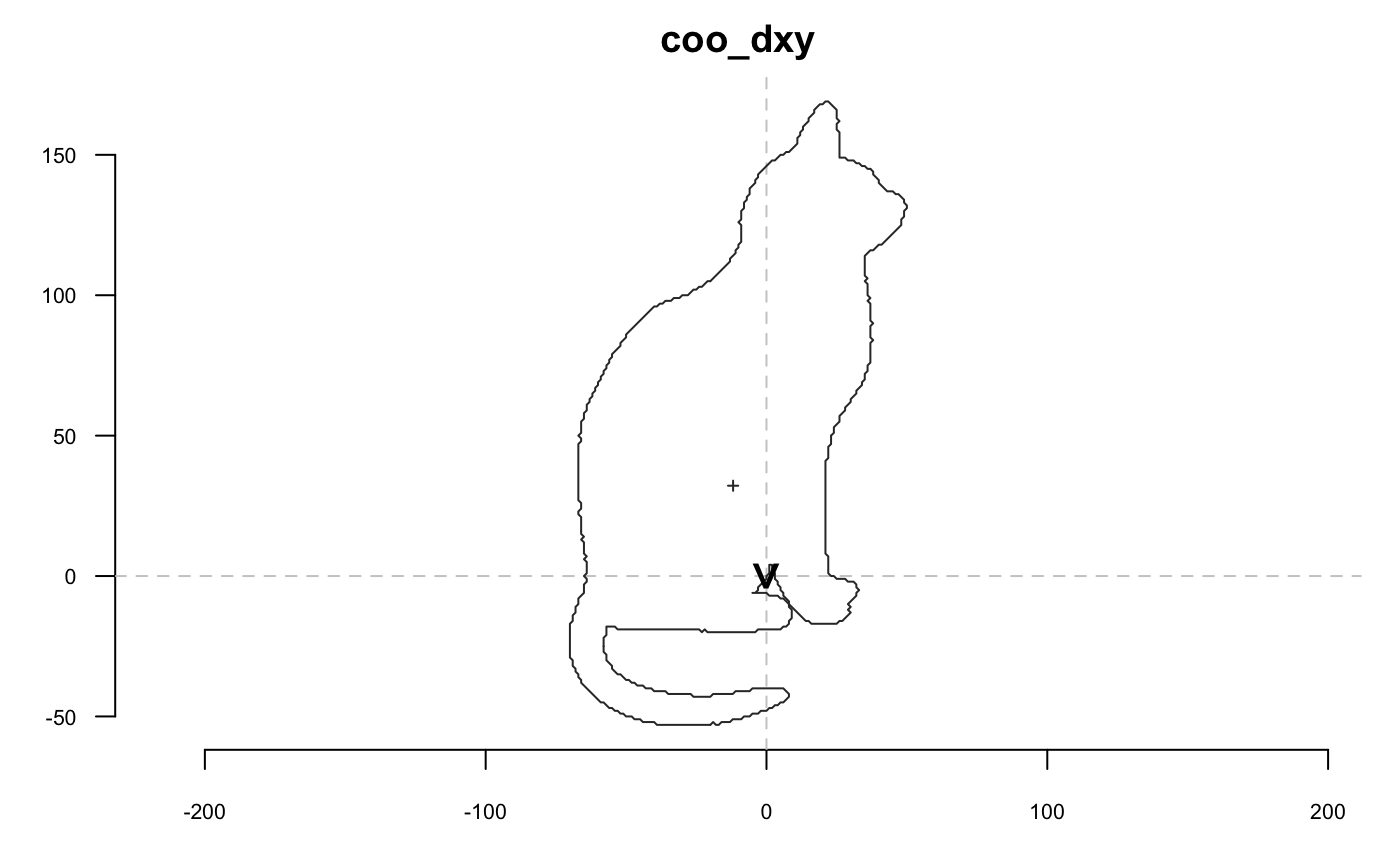
shp %>% coo_dxy %>% coo_plot(main="coo_dxy", cex.first.point = 2)

coo_force2close can be use to spread differences between the first and last point, and to force closing: