Calculate natural polynomial fits on open outlines

Calculates natural polynomial coefficients, through a linear model fit (see lm), from a matrix of (x; y) coordinates or an Opn object

Usage

npoly(x, ...)

# S3 method for default
npoly(x, degree, ...)

# S3 method for Opn
npoly(
  x,
  degree,
  baseline1 = c(-0.5, 0),
  baseline2 = c(0.5, 0),
  nb.pts = 120,
  ...
)

# S3 method for list
npoly(x, ...)

Arguments

x

a matrix (or a list) of (x; y) coordinates or an Opn object

...

useless here

degree

polynomial degree for the fit (the Intercept is also returned)

baseline1

numeric the \((x; y)\) coordinates of the first baseline by default \((x= -0.5; y=0)\)

baseline2

numeric the \((x; y)\) coordinates of the second baseline by default \((x= 0.5; y=0)\)

nb.pts

number of points to sample and on which to calculate polynomials

Value

when applied on a single shape, a list with components:

• coeff the coefficients (including the intercept)

• ortho whether orthogonal or natural polynomials were fitted

• degree degree of the fit (could be retrieved through coeff though)

• baseline1 the first baseline point (so far the first point)

• baseline2 the second baseline point (so far the last point)

• r2 the r2 from the fit

• mod the raw lm model

otherwise, an OpnCoe object.

See also

Other polynomials: opoly_i(), opoly()

Examples

data(olea)
o <- olea[1]
op <- opoly(o, degree=4)
op
#> $coeff
#> (Intercept)          x1          x2          x3          x4 
#>  0.20937101  0.01991936 -0.95319289 -0.03075138 -0.11975200 
#> 
#> $ortho
#> [1] TRUE
#> 
#> $degree
#> [1] 4
#> 
#> $baseline1
#> [1] -0.5  0.0
#> 
#> $baseline2
#> [1] 0.5 0.0
#> 
#> $r2
#> [1] 0.9986415
#> 
#> $mod
#> 
#> Call:
#> lm(formula = coo[, 2] ~ x)
#> 
#> Coefficients:
#> (Intercept)           x1           x2           x3           x4  
#>     0.20937      0.01992     -0.95319     -0.03075     -0.11975  
#> 
#> 
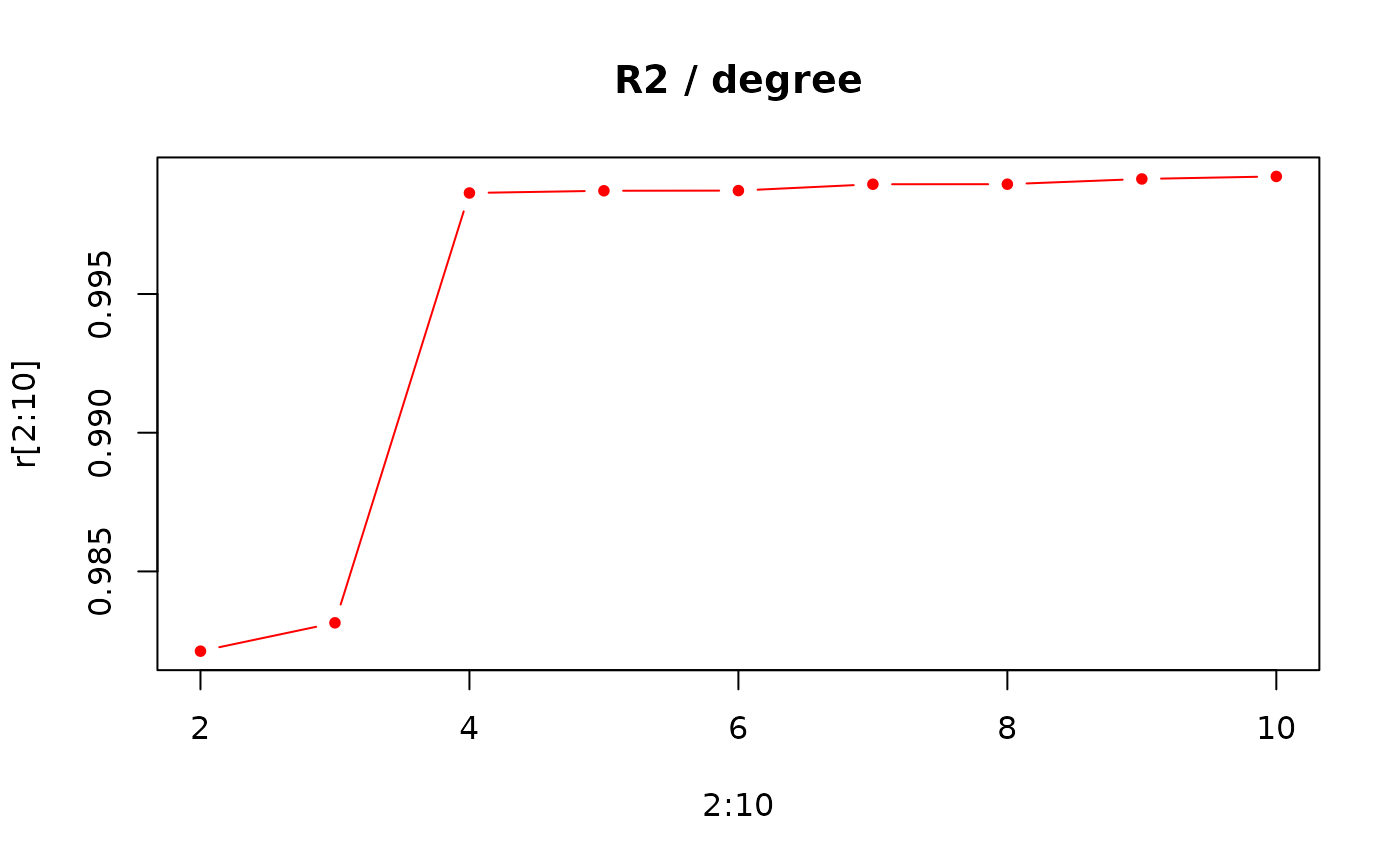
# shape reconstruction
opi <- opoly_i(op)
coo_plot(o)
coo_draw(opi, border="red")

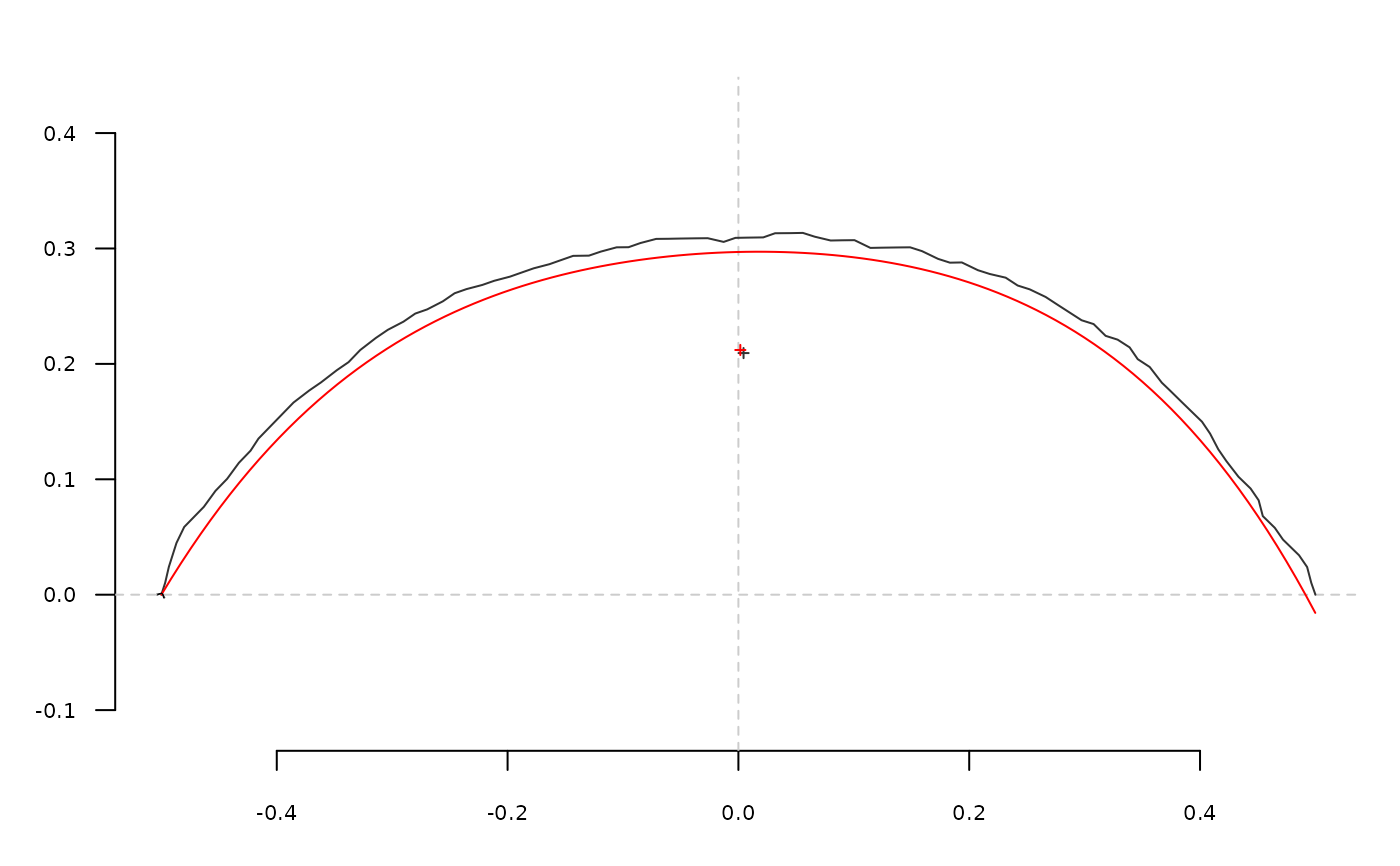# R2 for degree 1 to 10
r <- numeric()
for (i in 1:10) { r[i] <- npoly(o, degree=i)$r2 }
plot(2:10, r[2:10], type='b', pch=20, col='red', main='R2 / degree')