Elliptical Fourier transform (and its normalization)

efourier computes Elliptical Fourier Analysis (or Transforms or EFT) from a matrix (or a list) of (x; y) coordinates. efourier_norm normalizes Fourier coefficients. Read Details carefully.

Usage

efourier(x, ...)

# S3 method for default
efourier(x, nb.h, smooth.it = 0, ...)

# S3 method for Out
efourier(x, nb.h, smooth.it = 0, norm = TRUE, start = FALSE, ...)

# S3 method for list
efourier(x, ...)

efourier_norm(ef, start = FALSE)

Arguments

x: A list or a matrix of coordinates or a Out object
...: useless here
nb.h: integer. The number of harmonics to use. If missing, 12 is used on shapes; 99 percent of harmonic power on Out objects, both with messages.
smooth.it: integer. The number of smoothing iterations to perform.
norm: whether to normalize the coefficients using efourier_norm
start: logical. For efourier whether to consider the first point as homologous; for efourier_norm whether to conserve the position of the first point of the outline.
ef: list with a_n, b_n, c_n and d_n Fourier coefficients, typically returned by efourier

Value

For efourier, a list with components: an, bn, cn, dn harmonic coefficients, plus ao and co. The latter should have been named a0 and c0 in Claude (2008) but I (intentionnaly) propagated the error.

For efourier_norm, a list with components: A, B, C, D

for harmonic coefficients, plus size, the magnitude of the semi-major axis of the first fitting ellipse, theta angle, in radians, between the starting and the semi-major axis of the first fitting ellipse, psi orientation of the first fitting ellipse, ao and do, same as above, and lnef that is the concatenation of coefficients.

Details

For the maths behind see the paper in JSS.

Normalization of coefficients has long been a matter of trouble, and not only for newcomers. There are two ways of normalizing outlines: the first, and by far the most used, is to use a "numerical" alignment, directly on the matrix of coefficients. The coefficients of the first harmonic are consumed by this process but harmonics of higher rank are normalized in terms of size and rotation. This is sometimes referred as using the "first ellipse", as the harmonics define an ellipse in the plane, and the first one is the mother of all ellipses, on which all others "roll" along. This approach is really convenient as it is done easily by most software (if not the only option) and by Momocs too. It is the default option of efourier.

But here is the pitfall: if your shapes are prone to bad aligments among all the first ellipses, this will result in poorly (or even not at all) "homologous" coefficients. The shapes particularly prone to this are either (at least roughly) circular and/or with a strong bilateral symmetry. You can try to use stack on the Coe object returned by efourier. Also, and perhaps more explicitely, morphospace usually show a mirroring symmetry, typically visible when calculated in some couple of components (usually the first two).

If you see these upside-down (or 180 degrees rotated) shapes on the morphospace, you should seriously consider aligning your shapes before the efourier step, and performing the latter with norm = FALSE.

Such a pitfall explains the (quite annoying) message when passing efourier with just the Out.

You have several options to align your shapes, using control points (or landmarks), by far the most time consuming (and less reproducible) but possibly the best one too when alignment is too tricky to automate. You can also try Procrustes alignment (see fgProcrustes) through their calliper length (see coo_aligncalliper), etc. You should also make the first point homologous either with coo_slide or coo_slidedirection to minimize any subsequent problems.

I will dedicate (some day) a vignette or a paper to this problem.

Note

Directly borrowed for Claude (2008).

Silent message and progress bars (if any) with options("verbose"=FALSE).

References

Claude, J. (2008) Morphometrics with R, Use R! series, Springer 316 pp. Ferson S, Rohlf FJ, Koehn RK. 1985. Measuring shape variation of two-dimensional outlines. Systematic Biology 34: 59-68.

Examples

# single shape
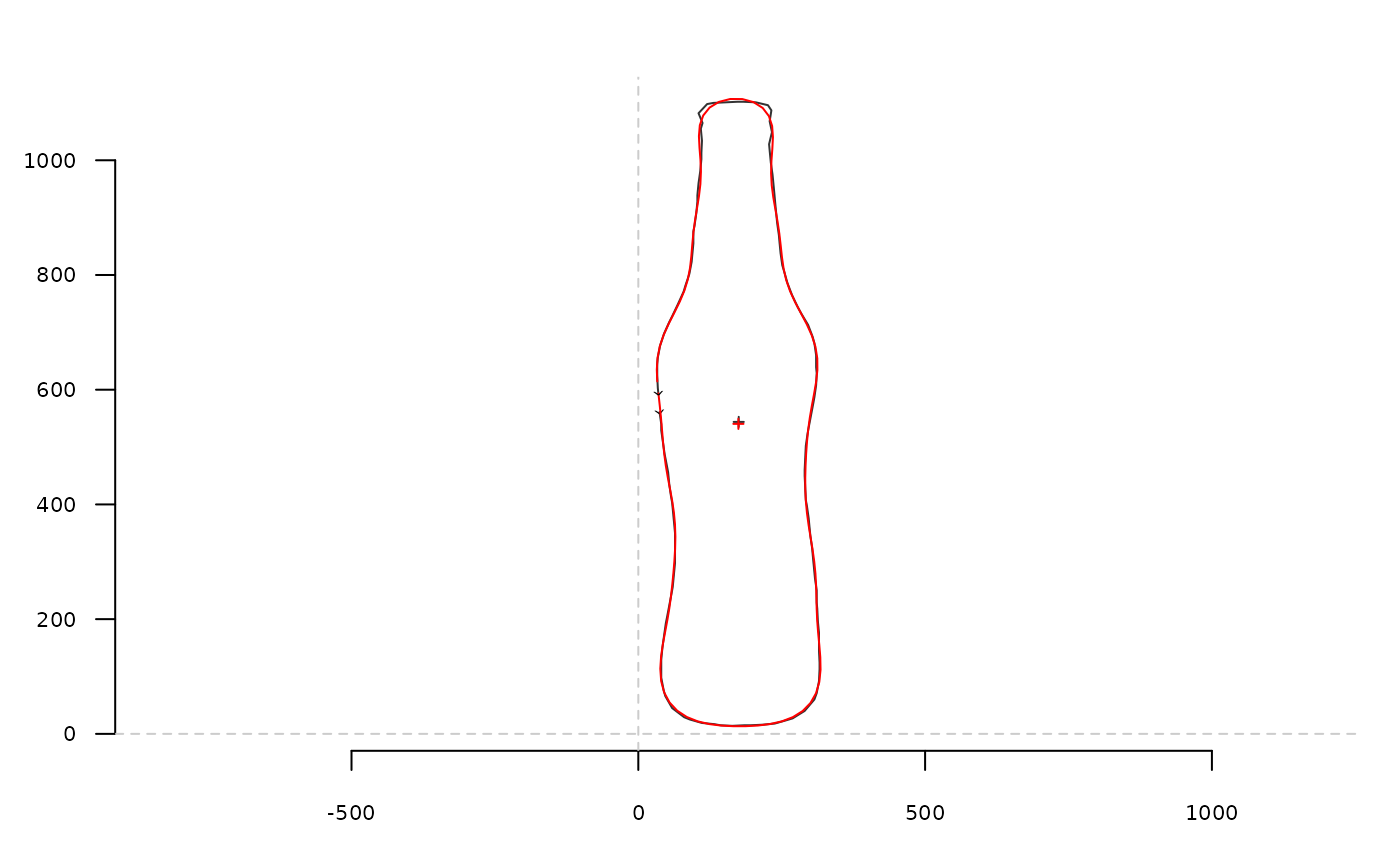
coo <- bot[1]
coo_plot(coo)
ef <- efourier(coo, 12)
# same but silent
efourier(coo, 12, norm=TRUE)
#> $an
#>  [1] -143.1142910    5.2925309   22.9922936  -11.3596452  -14.9412217
#>  [6]   -5.4200881    5.7177112    0.4509076    0.3107020   -3.1633079
#> [11]    0.2814646    3.4927761
#> 
#> $bn
#>  [1] -13.8501141 -21.8994092  11.4235084  13.5870435 -12.6401807   2.5050679
#>  [7]   5.1968464  -0.5366171  -1.0431706   1.0823659   2.3427969   0.1022387
#> 
#> $cn
#>  [1]  64.44753053  -3.15375656 -17.96822626   5.76052596   7.17390949
#>  [6]  -2.98410094  -1.20013013   1.18299684  -0.36305436  -0.46782525
#> [11]   0.67134872   0.08954658
#> 
#> $dn
#>  [1] -484.90299209   -1.04774048   42.07408510    3.40654863   -9.19128141
#>  [6]   -2.99359284    0.96722479    2.22582484    0.02026172   -2.26134728
#> [11]   -0.04679906    0.80569603
#> 
#> $ao
#> [1] 349.02
#> 
#> $co
#> [1] 1080.921
#> 
# inverse EFT
efi <- efourier_i(ef)
coo_draw(efi, border='red', col=NA)


# on Out
bot %>% slice(1:5) %>% efourier
#> 'norm=TRUE' is used and this may be troublesome. See ?efourier #Details
#> 'nb.h' set to 10 (99% harmonic power)
#> An OutCoe object [ elliptical Fourier analysis ]
#> --------------------
#>  - $coe: 5 outlines described, 10 harmonics
#> # A tibble: 5 × 2
#>   type   fake 
#>   <fct>  <fct>
#> 1 whisky a    
#> 2 whisky a    
#> 3 whisky a    
#> 4 whisky a    
#> 5 whisky a