Full Generalized Procrustes alignment between shapes

Directly borrowed from Claude (2008), called there the fgpa2 function.

Usage

fgProcrustes(x, tol, coo)

Arguments

x

an array, a list of configurations, or an Out, Opn or Ldk object

tol

numeric when to stop iterations

coo

logical, when working on Out or Opn, whether to use $coo rather than $ldk

Value

a list with components:

• rotated array of superimposed configurations

• iterationnumber number of iterations

• Q convergence criterion

• Qi full list of Q

• Qd difference between successive Q

• interproc.dist minimal sum of squared norms of pairwise differences between all shapes in the superimposed sample

• mshape mean shape configuration

• cent.size vector of centroid sizes.

or an Out, Opn or an Ldk object.

Details

If performed on an Out or an Opn object, will try to use the $ldk slot, if landmarks have been previousy defined, then (with a message) on the $coo slot, but in that case, all shapes must have the same number of coordinates (coo_sample may help).

Note

Slightly less optimized than procGPA in the shapes package (~20% on my machine). Will be optimized when performance will be the last thing to improve! Silent message and progress bars (if any) with options("verbose"=FALSE).

References

Claude, J. (2008). Morphometrics with R. Analysis (p. 316). Springer.

See also

Other procrustes functions: fProcrustes(), fgsProcrustes(), pProcrustes()

Examples

# on Ldk
w <- wings %>% slice(1:5) # for the sake of speed
stack(w)

fgProcrustes(w, tol=0.1) %>% stack()
#> iteration:  1 	gain: 77.967 
#> iteration:  2 	gain: 0.00039082 


# on Out
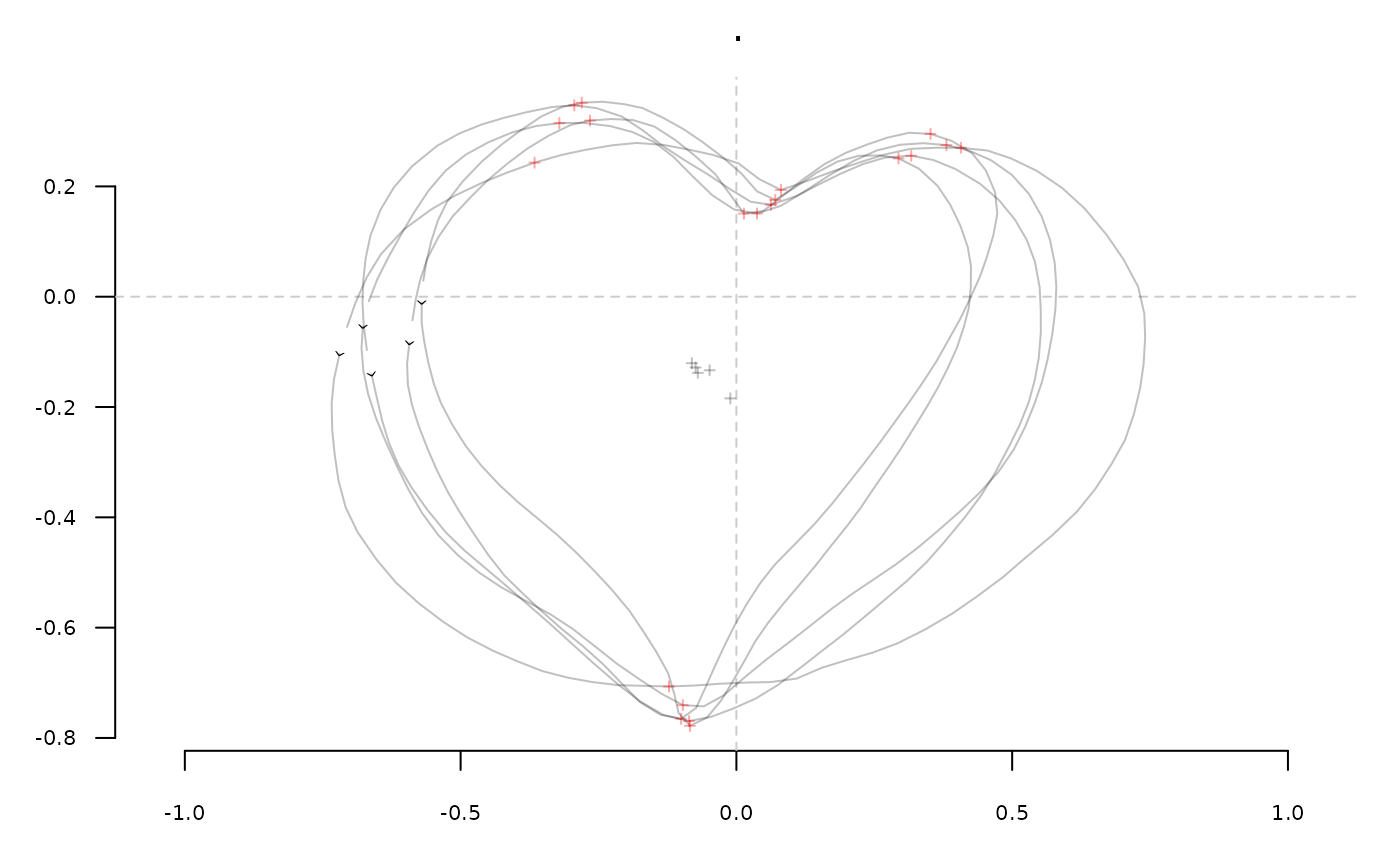
h <- hearts %>% slice(1:5) # for the sake of speed
stack(h)

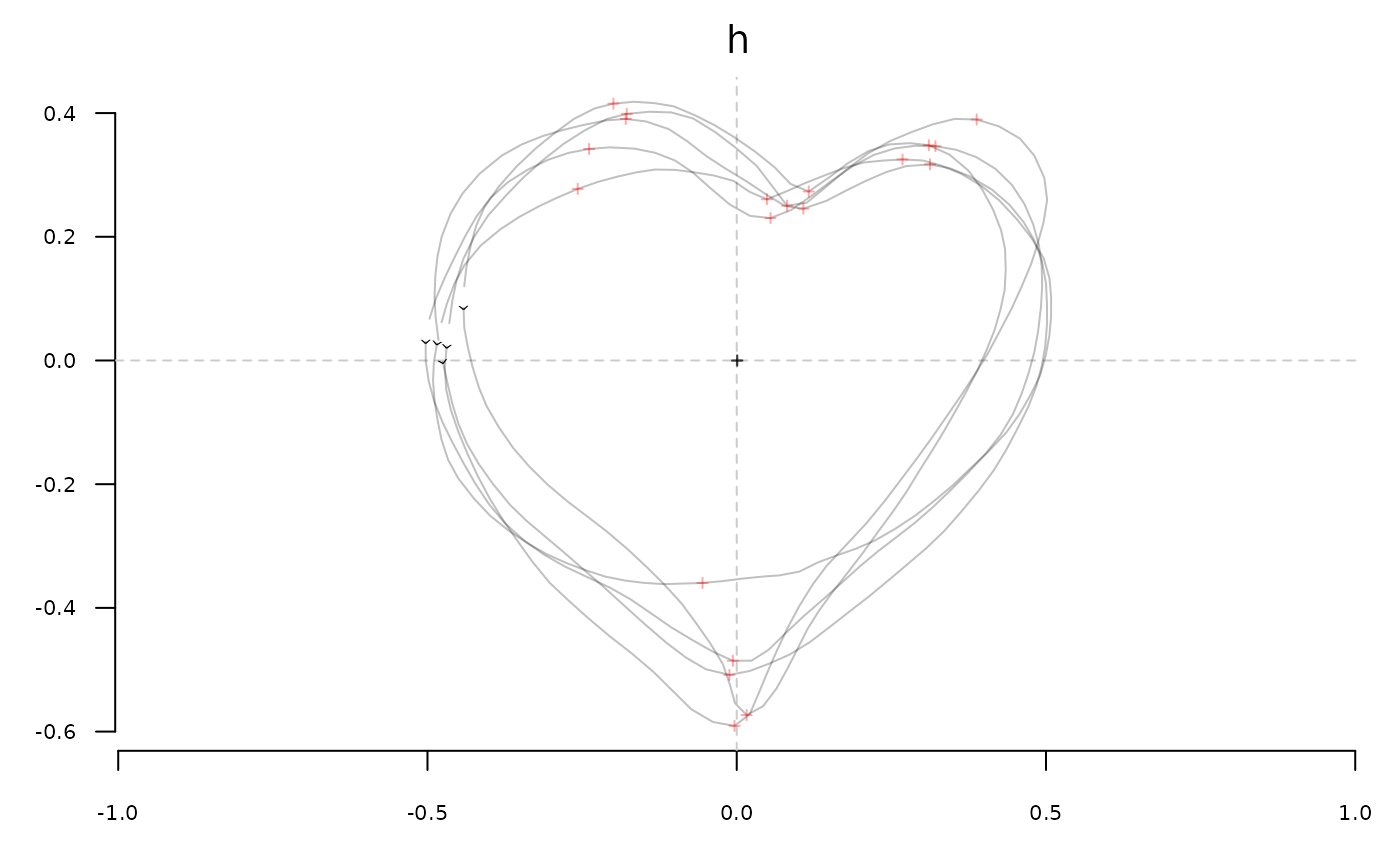fgProcrustes(h) %>%  stack()
#> iteration:  1 	gain: 8.1326 
#> iteration:  2 	gain: 0.00031224 
#> iteration:  3 	gain: 4.8293e-05 
#> iteration:  4 	gain: 1.0158e-06 
#> iteration:  5 	gain: 4.1771e-05 
#> iteration:  6 	gain: 7.9575e-06 
#> iteration:  7 	gain: 9.2944e-06 
#> iteration:  8 	gain: 3.1971e-07 
#> iteration:  9 	gain: 5.6429e-06 
#> iteration:  10 	gain: 3.6475e-06 
#> iteration:  11 	gain: 1.0455e-06 
#> iteration:  12 	gain: 4.6442e-08 
#> iteration:  13 	gain: 3.9276e-07 
#> iteration:  14 	gain: 5.6006e-07 
#> iteration:  15 	gain: 3.5497e-07 
#> iteration:  16 	gain: 2.2619e-08 
#> iteration:  17 	gain: 1.6228e-07 
#> iteration:  18 	gain: 1.662e-07 
#> iteration:  19 	gain: 8.6435e-08 
#> iteration:  20 	gain: 6.7107e-09 
#> iteration:  21 	gain: 3.6428e-08 
#> iteration:  22 	gain: 4.0699e-08 
#> iteration:  23 	gain: 2.2641e-08 
#> iteration:  24 	gain: 2.0915e-09 
#> iteration:  25 	gain: 9.3406e-09 
#> iteration:  26 	gain: 1.0441e-08 
#> iteration:  27 	gain: 5.8207e-09 
#> iteration:  28 	gain: 6.1735e-10 
#> iteration:  29 	gain: 2.312e-09 
#> iteration:  30 	gain: 2.6457e-09 
#> iteration:  31 	gain: 1.502e-09 
#> iteration:  32 	gain: 1.793e-10 
#> iteration:  33 	gain: 5.7701e-10 
#> iteration:  34 	gain: 6.7226e-10 
#> iteration:  35 	gain: 3.8692e-10 
#> iteration:  36 	gain: 5.1135e-11