Euclidean distance helpers

A little tribe to help with euclidean distances calculations

ed(x, y)

edi(x, y, r = 0.5)

ed_pw(x, y)

ed_nearest(x, y)

ed_furthest(x, y)

ed_calliper(x)

ed_minrad(x)

Arguments

x, y

coo_single, matrices or vectors of length 2 (when sensible)
r

numeric how much of the distance d(x -> y) should we travel?

Functions

  • ed: calculates euclidean distance between two points

  • edi: calculates intermediate position between two points

  • ed_pw: calculates pairwise distances between two shapes

  • ed_nearest: calculates closest point to y from x

  • ed_furthest: calculates furthest point to y from x

  • ed_calliper: find calliper (max pairwise ed) length

  • ed_minrad: find minimal radius (min dist to centroid)

See also

Other geometry: geometry

Examples

x <- c(0, 0)
y <- c(1, 1)

ed(x, y) # sqrt(2)
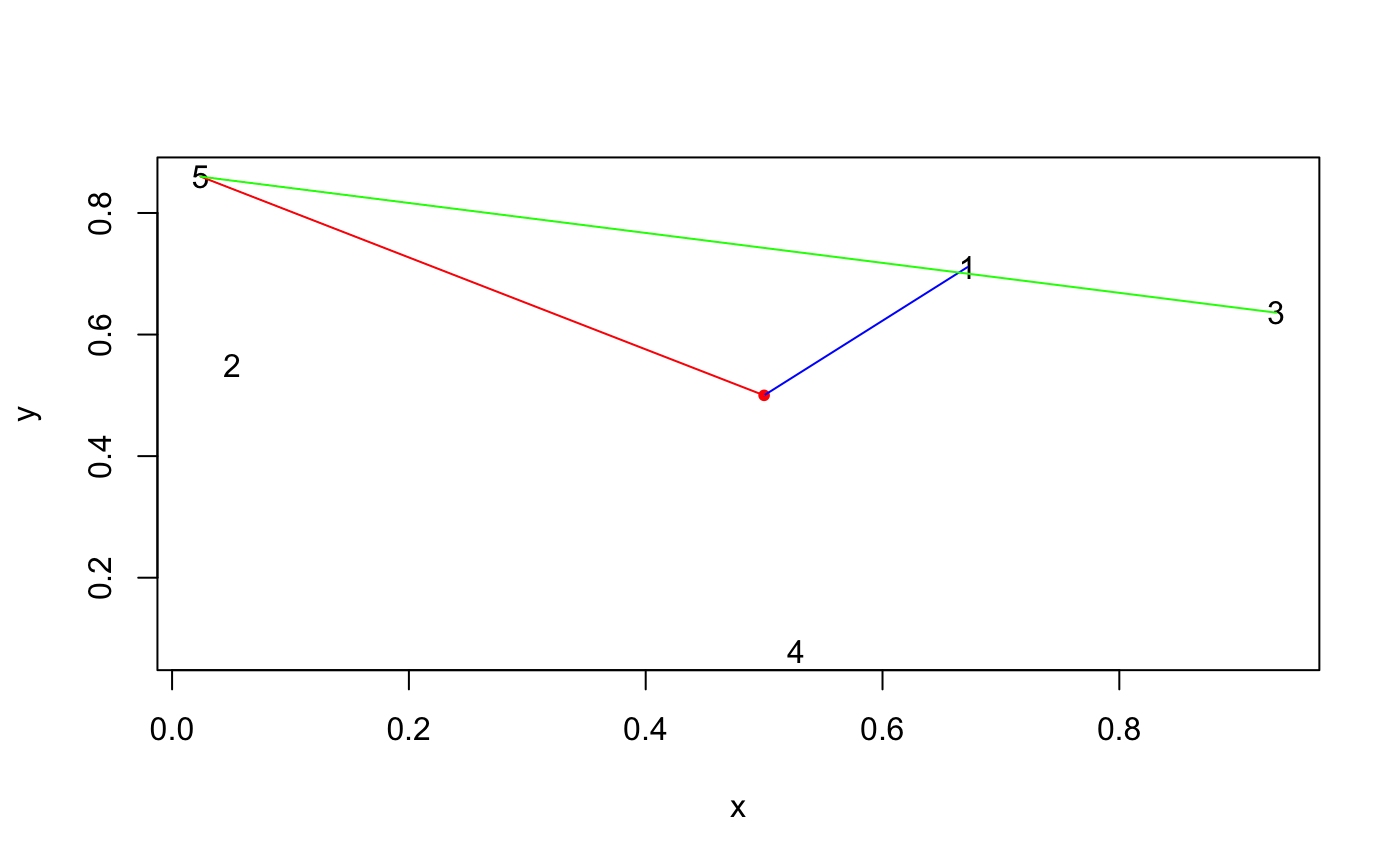
#> [1] 1.414214
edi(x, y, 0.25) # c(0.25, 0.25)
#> [1] 0.25 0.25

bot %>% dplyr::slice(1:2) %>% coo_sample(12)  %>% dplyr::pull(coo) -> b
ed_pw(b[[1]], b[[2]])
#>  [1] 30.52868 20.59126 16.27882 13.03840 18.43909 12.52996 63.06346 73.05477
#>  [9] 78.23043 96.76776 77.36924 45.45327
# checking
purrr::map_dbl(1:12, ~ed(b[[1]][.x, ], b[[2]][.x, ]))
#>  [1] 30.52868 20.59126 16.27882 13.03840 18.43909 12.52996 63.06346 73.05477
#>  [9] 78.23043 96.76776 77.36924 45.45327

bot %>% pick(1) %>% ed_nearest(c(0, 0))
#> $d
#> [1] 74.20243
#> 
#> $ids
#> x30 
#>  30 
#> 

# nearest and furthest points

set.seed(2329) # for the sake of reproducibility when building the pkg
foo <- tibble::tibble(x=runif(5), y=runif(5))
z <- c(0.5, 0.5)
plot(foo, pch="")
text(foo, labels=1:5)
points(z[1], z[2], col="red", pch=20)

(nearest <- ed_nearest(foo, z))
#> $d
#> [1] 0.2719217
#> 
#> $ids
#> x1 
#>  1 
#> 
segments(z[1], z[2],
         as.numeric(foo[nearest$id, 1]), as.numeric(foo[nearest$id, 2]), col="blue")

(furthest <- ed_furthest(foo, z))
#> $d
#> [1] 0.5968936
#> 
#> $ids
#> x5 
#>  5 
#> 
segments(z[1], z[2],
         as.numeric(foo[furthest$id, 1]), as.numeric(foo[furthest$id, 2]), col="red")


(calli <- ed_calliper(foo))
#> $d
#> [1] 0.9358646
#> 
#> $ids
#> [1] 3 5
#> 
segments(as.numeric(foo[calli$ids[1], 1]), as.numeric(foo[calli$ids[1], 2]),
         as.numeric(foo[calli$ids[2], 1]), as.numeric(foo[calli$ids[2], 2]), col="green")