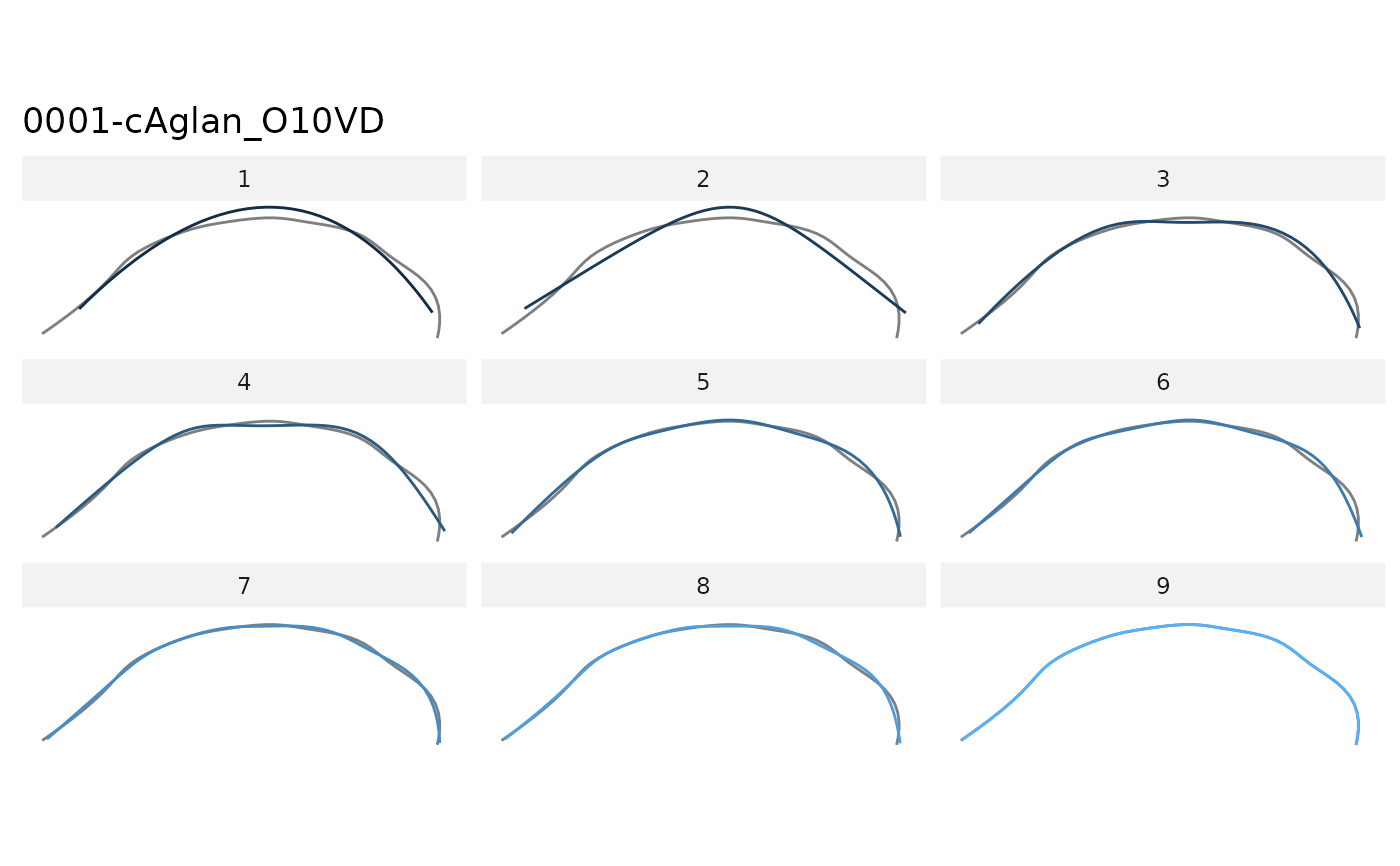
Calculate and displays reconstructed shapes using a range of harmonic number. Compare them visually with the maximal fit. This explicitely demonstrates how robust efourier is compared to tfourier and rfourier.
Usage
calibrate_reconstructions_efourier(x, id, range = 1:9)
calibrate_reconstructions_rfourier(x, id, range = 1:9)
calibrate_reconstructions_tfourier(x, id, range = 1:9)
calibrate_reconstructions_sfourier(x, id, range = 1:9)
calibrate_reconstructions_npoly(
x,
id,
range = 2:10,
baseline1 = c(-1, 0),
baseline2 = c(1, 0)
)
calibrate_reconstructions_opoly(
x,
id,
range = 2:10,
baseline1 = c(-1, 0),
baseline2 = c(1, 0)
)
calibrate_reconstructions_dfourier(
x,
id,
range = 2:10,
baseline1 = c(-1, 0),
baseline2 = c(1, 0)
)Arguments
- x
the
Cooobject on which to calibrate_reconstructions- id
the shape on which to perform calibrate_reconstructions
- range
vector of harmonics on which to perform calibrate_reconstructions
- baseline1
\((x; y)\) coordinates for the first point of the baseline
- baseline2
\((x; y)\) coordinates for the second point of the baseline
See also
Other calibration:
calibrate_deviations(),
calibrate_harmonicpower(),
calibrate_r2()
Examples
### On Out
shapes %>%
calibrate_reconstructions_efourier(id=1, range=1:6)
 # you may prefer efourier...
shapes %>%
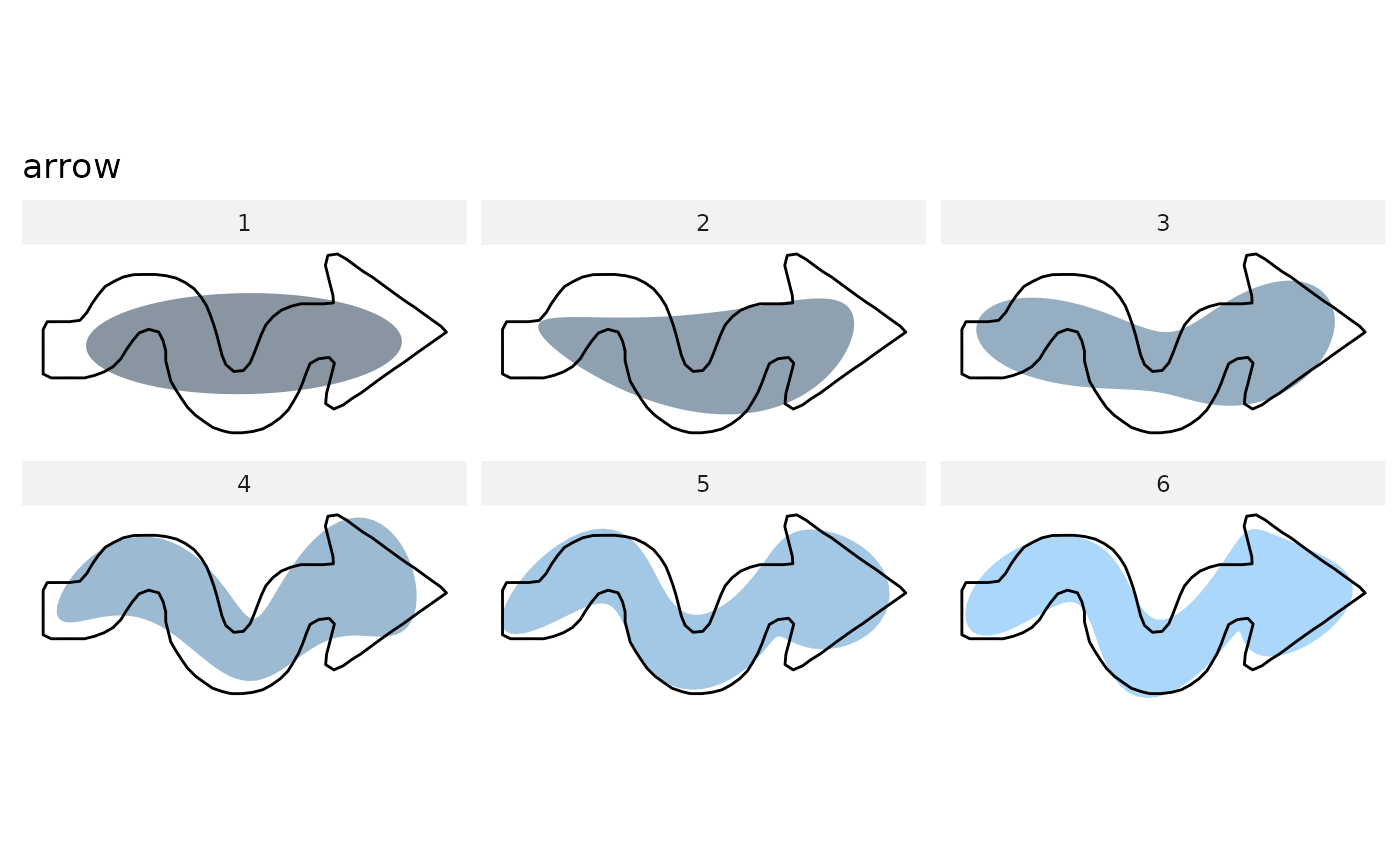
calibrate_reconstructions_tfourier(id=1, range=1:6)
# you may prefer efourier...
shapes %>%
calibrate_reconstructions_tfourier(id=1, range=1:6)
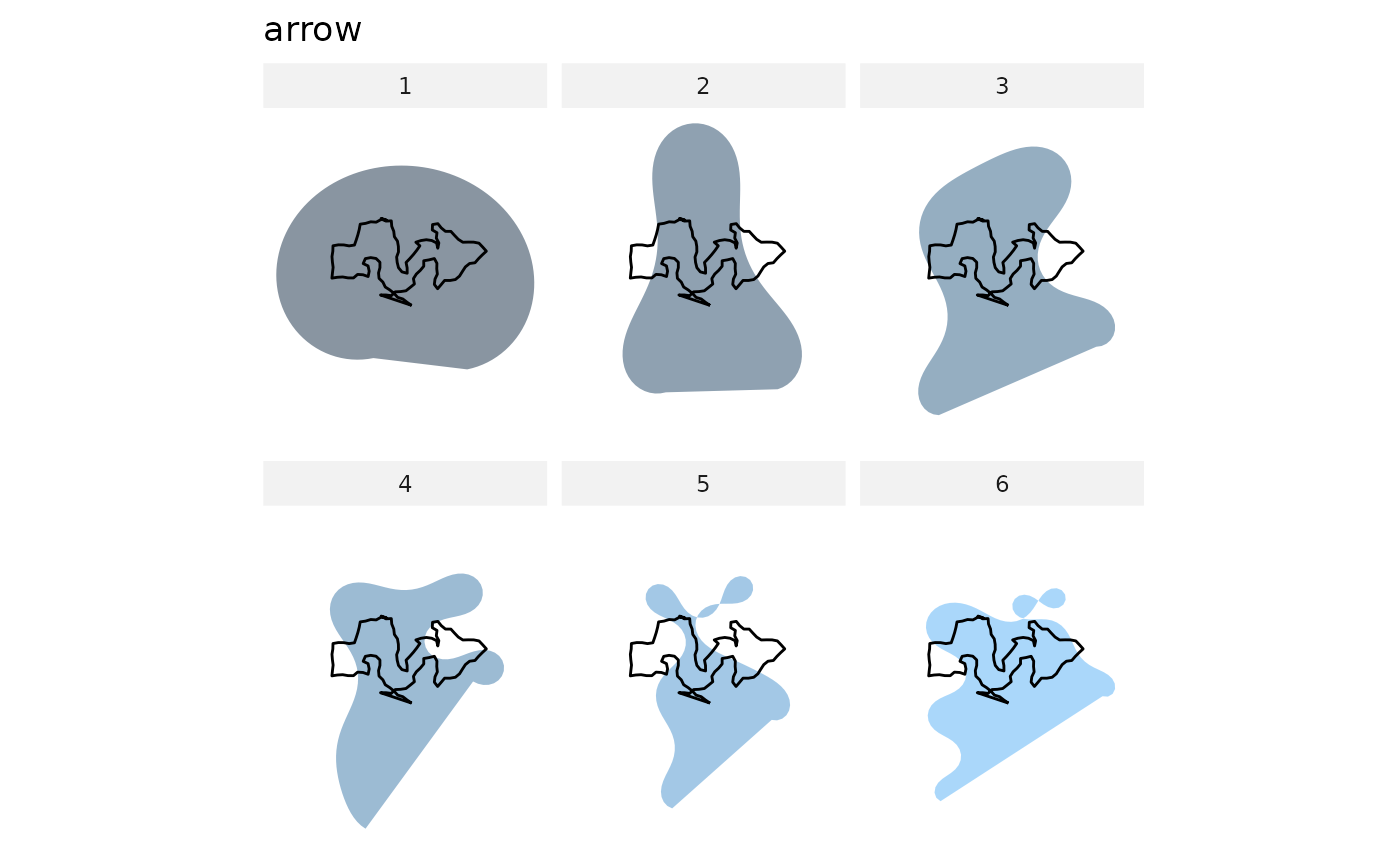 #' you may prefer efourier...
shapes %>%
calibrate_reconstructions_rfourier(id=1, range=1:6)
#' you may prefer efourier...
shapes %>%
calibrate_reconstructions_rfourier(id=1, range=1:6)
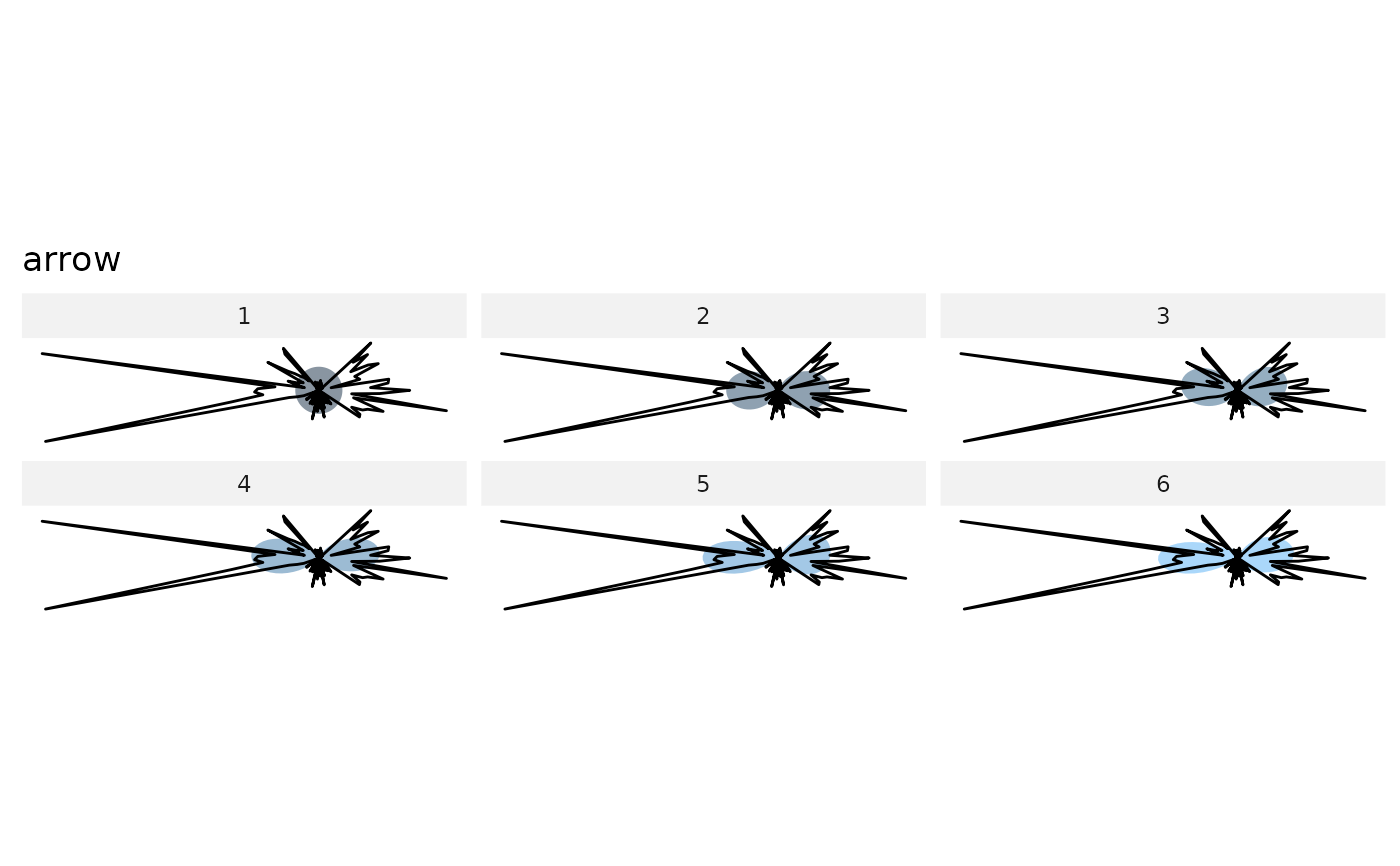 #' you may prefer efourier... # todo
#shapes %>%
# calibrate_reconstructions_sfourier(id=5, range=1:6)
### On Opn
olea %>%
calibrate_reconstructions_opoly(id=1)
#' you may prefer efourier... # todo
#shapes %>%
# calibrate_reconstructions_sfourier(id=5, range=1:6)
### On Opn
olea %>%
calibrate_reconstructions_opoly(id=1)
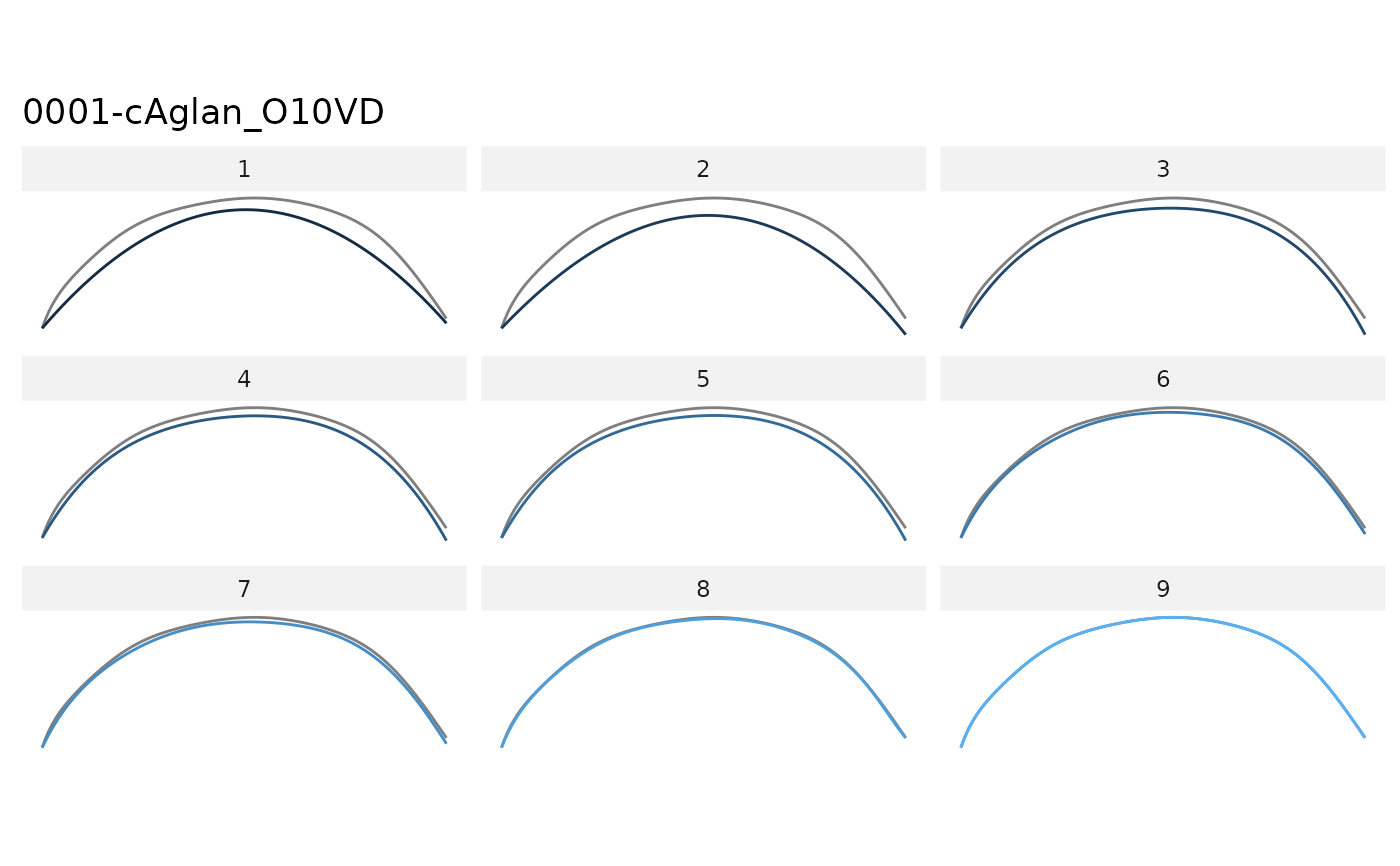 olea %>%
calibrate_reconstructions_npoly(id=1)
olea %>%
calibrate_reconstructions_npoly(id=1)
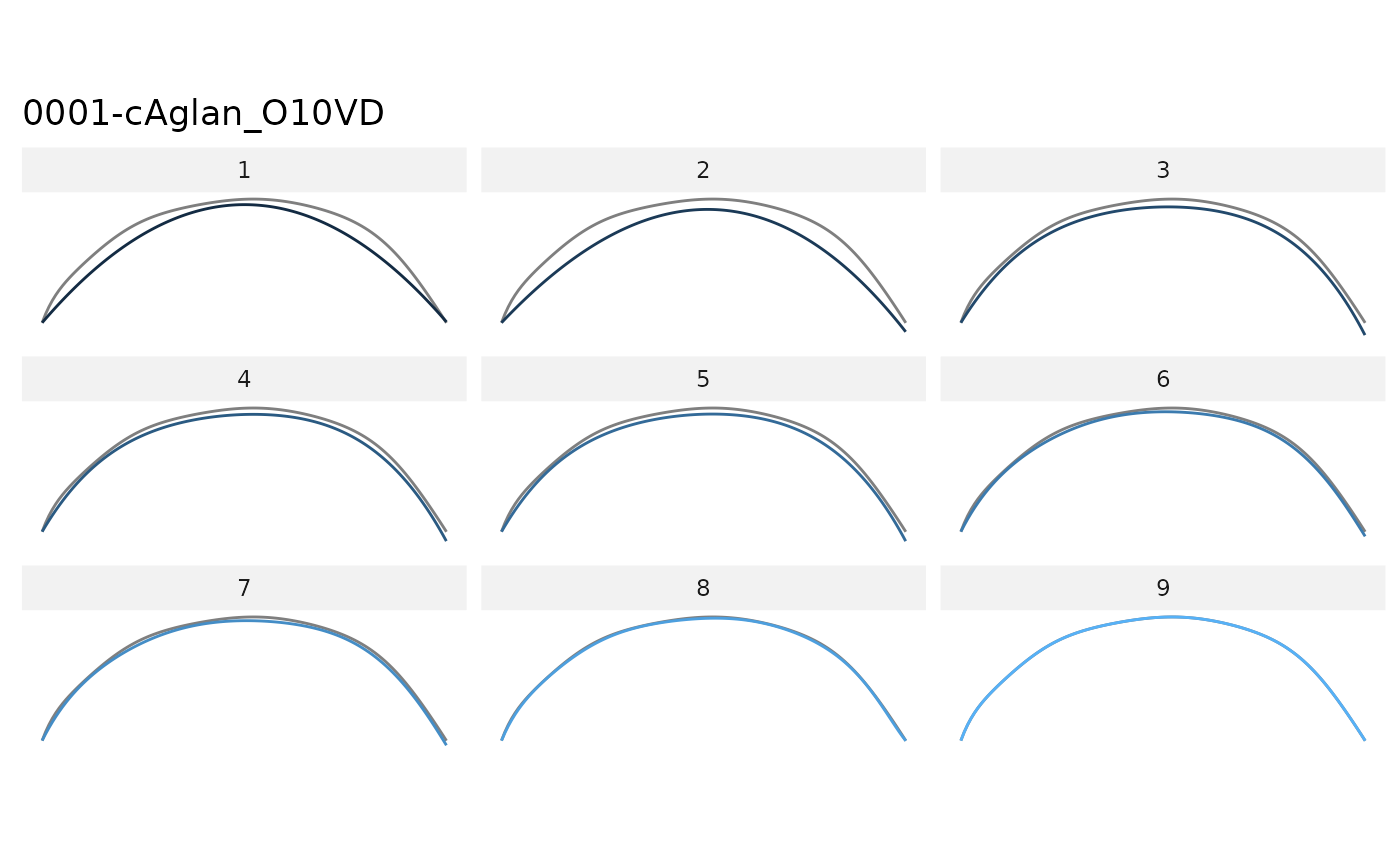 olea %>%
calibrate_reconstructions_dfourier(id=1)
olea %>%
calibrate_reconstructions_dfourier(id=1)